บทที่ 8 การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
ลักษณะการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
.gif)
ภาพที่ 1 การสั่นของมวลติดปลายสปริง
.gif)
ภาพที่ 2 การแกว่งของลูกตุ้ม
ลักษณะการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
(Simple Harmonic Motion : SHM) คือ การเคลื่อนที่กลับไปมาซ้ำทางเดิมโดยผ่านตำแหน่งสมดุล (Equilibrium position) โดยไม่มีการสูญเสียพลังงาน (แอมพลิจูดและคาบของการเคลื่อนที่คงตัว) เช่น การเคลื่อนที่ของวัตถุติดปลายสปริง (ภาพที่ 1) การสั่นของสายเครื่องดนตรี การแกว่งของลูกตุ้มนาฬิกา (ภาพที่ 2) เป็นต้น
.png)
ภาพที่ 3 แสดงตำแหน่งสมดุล
Q : ตำแหน่งสมดุล (Equilibrium position) คือตำแหน่งใด
A : ตำแหน่งสมดุล คือ ตำแหน่งที่วัตถุอยู่ในสภาพสมดุล เมื่อวัตถุเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายจะเป็นตำแหน่งที่มีความเร็วมากที่สุดและมีความเร่งเป็นศูนย์
.png)
ภาพที่ 4 แสดงวัตถุที่เคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
เราจะศึกษาการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายจากภาพที่ 8.4 โดยกำหนดให้ทิศทางขวาเป็นบวก และทิศทางซ้ายเป็นลบ
.jpeg)
และเนื่องจากวัตถุเริ่มเคลื่อนที่ที่ตำแหน่ง x = A ความเร็วของวัตถุจึงเป็นศูนย์
เนื่องจากพื้นไม่มีแรงเสียดทาน และสปริงก็ไม่ออกแรงกระทำต่อวัตถุ ดังนั้นที่ตำแหน่ง x = 0 นี้ วัตถุจึงสามารถรักษาสภาพการเคลื่อนที่ตามกฎข้อที่ 1 ของนิวตันไว้ได้ วัตถุจึงยังคงสามารถเคลื่อนที่ต่อไปทางซ้ายได้
มีข้อน่าสังเกตว่า ขนาดของการกระจัดมากที่สุดของวัตถุไม่ว่าจะเป็นทางซ้ายหรือขวาจะเท่ากัน คือ เป็น A เนื่องจากมีแรงมากระทำต่อวัตถุเพียงแรงเดียว คือ แรงจากสปริง ซึ่งมีทิศไปทางขวา วัตถุจึงเคลื่อนที่กลับไปทางขวาด้วยอิทธิพลของแรงนี้
ดังนั้น การเคลื่อนที่ของวัตถุจึงกลับไปกลับมาซ้ำทางเดิม คือ จาก 4 (b) → 4 (c) → 4 (d) → 4 (e) → 4 (b) (ตำแหน่งเดียวกับ 4 (f)) เป็นอย่างนี้เรื่อยไป จึงเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย หรือ SHM.
เนื่องจากการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายเป็นการเคลื่อนที่ที่มีการเปลี่ยนแปลงความเร็วของวัตถุที่ตำแหน่งต่าง ๆ
แสดงว่ามีความเร่ง วัตถุจึงมีการเคลื่อนที่เป็นไปตามกฎข้อที่ 2 ของนิวตัน ƩF = Sma....(1) และแรงที่ทำให้วัตถุเคลื่อนที่
คือ แรงดึงกลับของสปริงF = -kx แทนค่า
F ใน
(1) จะได้ว่า
-kx = ma จัดรูปสมการได้เป็น
a = -(k/m)x จะเห็นได้ว่า
ความเร่งมีขนาดแปรผันตรงกับการกระจัดแต่มีทิศตรงกันข้าม (มีค่าเป็นลบ)
.jpeg)
สรุปลักษณะการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
.jpeg)
.gif)
.jpeg)
ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
.jpeg)
ภาพที่ 5 แสดงตำแหน่งสมดุล การกระจัดและแอมพลิจูดของมวลติดปลายสปริง
.png)
ภาพที่ 6 แสดงตำแหน่งสมดุล การกระจัดและแอมพลิจูดของลูกตุ้ม
1.การกระจัด (displacement) คือ ระยะที่วัตถุเคลื่อนที่ไปได้โดยวัดจากตำแหน่งสมดุลไปจนถึงตำแหน่งของวัตถุ ในกรณีที่วัตถุเคลื่อนที่ในแนวระดับแทนด้วยสัญลักษณ์ x และเมื่อวัตถุเคลื่อนที่ในแนวดิ่งแทนด้วยสัญลักษณ์ y มีหน่วยเป็นเมตร (m)
2.แอมพลิจูด (amplitude) คือ ระยะมากที่สุดที่วัตถุจะสามารถเคลื่อนที่ไปได้ โดยวัดจากตำแหน่งสมดุลไปจนถึงจุดปลาย มีค่าคงที่เสมอ แทนด้วยสัญลักษณ์ A มีหน่วยเป็นเมตร (m)
อาจจะพิจารณาได้ว่า แอมพลิจูด ก็คือ การกระจัดที่มีค่ามากที่สุดนั่นเอง
3. คาบ (period) คือ ช่วงเวลาที่วัตถุเคลื่อนที่ครบหนึ่งรอบ แทนด้วยสัญลักษณ์ T มีหน่วยเป็นวินาทีต่อรอบหรือวินาที (s)
4. ความถี่ (frequency ) คือ จำนวนรอบที่วัตถุเคลื่อนที่ได้ในหนึ่งหน่วยเวลา แทนด้วยสัญลักษณ์ f มีหน่วยเป็นรอบต่อวินาที (s-1 , 1/s ) หรือเฮิรตซ์ (Hz)
.jpeg)
ความสัมพันธ์ระหว่างคาบและความถี่ เป็นไปดังสมการ
.jpeg)
.png)
ภาพที่ 7 แสดงตำแหน่งการเคลื่อนที่ของมวลติดปลายสปริง
.png)
ภาพที่ 8 แสดงตำแหน่งการเคลื่อนที่ของลูกตุ้ม
Q : เราสามารถนับรอบของวัตถุที่มีการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายได้อย่างไร
A : วิธีการนับรอบการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายของวัตถุ หากวัตถุเริ่มเคลื่อนที่จากตำแหน่ง A → B → C → B → A หรือหากวัตถุเริ่มเคลื่อนจากตำแหน่ง C → B → A → B → C จึงถือว่าครบหนึ่งรอบ
การเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายเทียบกับการเคลื่อนที่แบบวงกลม
การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย มีลักษณะคล้ายกับการเคลื่อนที่แบบวงกลม กล่าวคือ มีการเคลื่อนที่กลับไปกลับมาซ้ำรอยเดิม มีการเคลื่อนที่แบบครบรอบ (Periodic motion) ดังนั้น การศึกษาปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายจึงสามารถศึกษาได้จากเงาของวัตถุที่เคลื่อนที่แบบวงกลมในระนาบดิ่งที่ตกกระทบไปยังระนาบในแนวดิ่งและในแนวระดับ กราฟการกระจัด กับเวลาอยู่ในรูปของฟังก์ชันไซน์ หรือโคไซน์ ดังภาพ
.jpeg)
ภาพที่ 9 แสดงเงาของการเคลื่อนที่แบบวงกลม
การกระจัดของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
.jpeg)
ภาพที่ 10 แสดงการกระจัดของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายเทียบกับการเคลื่อนที่แบบวงกลม
จากภาพที่ 10 วัตถุ Q เคลื่อนที่เป็นวงกลมรัศมี A ด้วยอัตราเร็วเชิงมุม ω เมื่อวัตถุ Q อยู่ที่ตำแหน่งหนึ่งซึ่งทำมุม θ กับแกน +x หากมีแสงฉายมาตามแนวแกน +y จะเกิดเงาของวัตถุ Q ที่ตำแหน่ง P โดยการกระจัดจากจุด O ถึงจุด P มีค่าเท่ากับ x = Acosθ หรือ x = Acosωt เนื่องจาก θ = ωt ในทำนองเดียวกัน หากมีแสงฉายมาตามแนวแกน +x จะเกิดเงาของวัตถุ Q ในแนวแกน y โดยการกระจัดจากจุด O ถึงเงาของวัตถุ Q มีค่าเท่ากับ y = Asinθ หรือ y = Asinωt ถ้าวัตถุ Q ยังเคลื่อนที่เป็นวงกลมต่อไป เงาของวัตถุ Q จะมีการเคลื่อนที่กลับไปกลับมาแบบฮาร์มอนิกอย่างง่าย
ความเร็วและความเร่งของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
.jpeg)
ภาพที่ 11 แสดงความเร็วของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายเทียบกับการเคลื่อนที่แบบวงกลม
จากภาพที่ 11 พิจารณาความเร็ว v ของวัตถุ Q ที่ตำแหน่งหนึ่งซึ่งทำมุม θ กับแกน +x เนื่องจาก Q มีการเคลื่อนที่เป็นวงกลม ความเร็ว v จึงอยู่ในแนวเส้นสัมผัสวงกลม (ลูกศรสีแดง) ซึ่งความเร็ว v เป็นความเร็วเชิงเส้นมีความสัมพันธ์กับความเร็วเชิงมุม ω ดังสมการ v = ωR ซึ่งในภาพ R = A ดังนั้น v = ωA เนื่องจาก A เป็นค่าการกระจัดที่มากที่สุด ค่าความเร็ว v = ωA จึงเป็นความเร็วสูงสุด vmax เมื่อพิจารณาความเร็วในแนวแกน x และแกน y โดยกำหนดให้ ทิศขึ้นและขวาเป็นบวก ส่วนทิศลงและซ้ายเป็นลบ จะได้ว่า vx = - vmaxsinθ และ vy = vmaxcosθ ตามลำดับ เมื่อแทนค่า vmax และ θ จะได้เป็น vx = - ωAsinωt และ vy = ωAcosωt ซึ่งสมการทั้งสองเป็นสมการความเร็วที่เป็นฟังก์ชันของเวลา
หากต้องการเปลี่ยนสมการฟังก์ชันของเวลา ให้เป็นสมการที่ขึ้นกับตำแหน่ง (การกระจัด) สามารถทำได้โดยใช้อัตราส่วนตรีโกณมิติมาพิจารณาดังในภาพที่ 11
.jpeg)
ภาพที่ 12 แสดงความเร่งของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายเทียบกับการเคลื่อนที่แบบวงกลม
จากภาพที่ 12 พิจารณาความเร่ง a ของวัตถุ Q ที่ตำแหน่งหนึ่งซึ่งทำมุม θ กับแกน +x เนื่องจาก Q มีการเคลื่อนที่เป็นวงกลม ความเร่ง a จึงอยู่ในแนวรัศมีของวงกลมโดยมีทิศเข้าหาจุดศูนย์กลางของวงกลม (ลูกศรสีแดง) ซึ่งความเร่ง a มีความสัมพันธ์กับความเร็วเชิงมุม ω ดังสมการ a = ω2R ซึ่งในภาพ R = A ดังนั้น a = ω2A เนื่องจาก A เป็นค่าการกระจัดที่มากที่สุด (แอมพลิจูด) ค่าความเร่ง a = ω2A จึงเป็นความเร่งสูงสุด amax เมื่อพิจารณาความเร่งในแนวแกน x และแกน y โดยกำหนดให้ ทิศขึ้นและขวาเป็นบวก ส่วนทิศลงและซ้ายเป็นลบ จะได้ว่า ax = - amaxcosθ และ ay = - amaxsinθ ตามลำดับ เมื่อแทนค่า amax และ θ จะได้เป็น ax = - ω2Acosωt และ ay = -ω2Asinωt ซึ่งสมการทั้งสองเป็นสมการความเร็วที่เป็นฟังก์ชันของเวลา
หากต้องการเปลี่ยนสมการฟังก์ชันของเวลา ให้เป็นสมการที่ขึ้นกับตำแหน่ง (การกระจัด) สามารถแทนค่าการกระจัด x = Acosωt และ y = Asinωt ในสมการ ax และ ay ดังในภาพที่ 12
กราฟแสดงความสัมพันธ์ของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
.jpeg)
.jpeg)
สรุป การกระจัด ความเร็วและความเร่งของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
.png)
.png)
การสั่นของมวลติดปลายสปริง
.png)
.png)
การแกว่งของลูกตุ้มอย่างง่าย
.png)
.png)
ความถี่ธรรมชาติ (natural frequency )
คือ ความถี่ในการแกว่งอย่างอิสระของวัตถุ
การสั่นพ้อง (resonance) เกิดขึ้นเมื่อวัตถุถูกกระทำด้วยแรงหรือสัญญาณที่มีความถี่เท่ากับหรือใกล้เคียงกับความถี่ธรรมชาติของวัตถุ วัตถุนั้นจะสั่นด้วยความถี่นั้นและด้วยแอมพลิจูดที่มีค่ามาก แต่ถ้าเป็นคลื่นเสียงก็จะทำให้เสียงดังมากขึ้น จนอาจทำให้วัตถุนั้นเสียหายหรืออาจเกิดความรำคาญได้
หา'ความถี่ (f) 'กัน
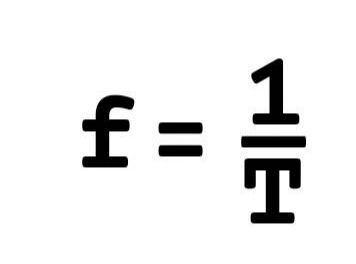
คาบ(T) วินาที(s)
โอเมก้า(ω) เรเดียนต่อวินาที(rad/s)
———————————
หา'คาบ (T) 'กัน
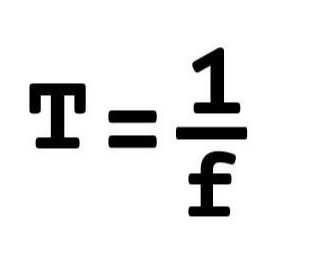
ความถี่(f) เฮิร์ต(Hz)
โอเมก้า(ω) เรเดียนต่อวินาที(rad/s)
———————————
หา' โอเมก้า (ω) 'กัน
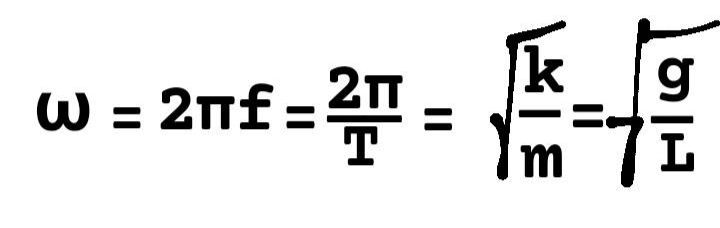
———————————
————————————————
———————————
————————————————
มวล(m) กิโลกรัม(kg)
โอเมก้า(ω) เรเดียนต่อวินาที(rad/s)
———————————
————————————————
ความยาวเชือก(L) กิโลกรัม(kg)
โอเมก้า(ω) เรเดียนต่อวินาที(rad/s)
———————————
หา'แรง'กัน
ΣF = ma
มวล(m) กิโลกรัม(kg)ความเร่ง(a) เมตรต่อวินาทีกำลัง2(m/s²)
แรง(ΣF) นิวตัน(N)
———————————
————————————————
-kx = ma
ค่าคงตัวสปริง(k) นิวตันเมตร(N/m)ระยะยืดหดของสปริง(x) เมตร(m)
มวล(m) กิโลกรัม (kg)
ความเร่ง(a) เมตรต่อวินาทีกำลัง2(m/s²)
———————————
จากสูตรของข้อนี้คือ -kx = ma เครื่องหมายลบในกฎของฮุกมีตความหมายว่า แรงดึงกลับของสปริงและการกระจัดของสปริงจะมีทิศตรงข้ามกันเสมอ
หา'ความเร่งสูงสุด (aₘₐₓ)'กัน
a = ω²x
ความเร่ง(a) เมตรต่อวินาทีกำลัง2(m/s²)โอเมก้า(ω) เรเดียนต่อวินาที(rad/s)
ระยะยืดหดของสปริง(x) เมตร(m)
———————————
จากสูตรของข้อนี้คือ a = -ω²x เครื่องหมายลบหมายความว่า การกระจัดและความเร่งจะมีทิศตรงข้ามกัน
หา'ความเร็วสูงสุด (vₘₐₓ)'กัน
v = ωA
ความเร็ว(v)เมตรต่อวินาที(m/s)โอเมก้า(ω)เรเดียนต่อวินาที(rad/s)
การกระจัดสูงสุด(A)เมตร(m)
———————————
แบบทดสอบเรื่อง การเคลื่อนที่แบบซิมเปิลฮาร์มอนิก
| Quizizz | circularmotion2016 | site.google | teamsnb |
|---|
แหล่งที่มา
https://sites.google.com/mst.ac.th/แหล่งที่มา แบบทดสอบ
https://quizizz.com/https://circularmotion2016.wordpress.com/
https://sites.google.com/
http://www.rmutphysics.com/charud/exercise-online/SHM/index11.htm
https://teamsnb.com/